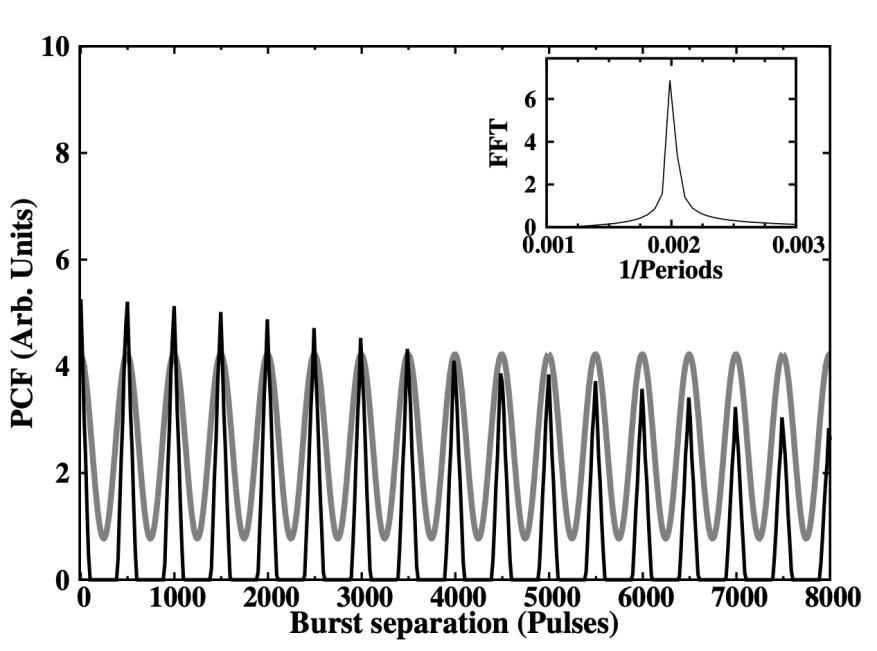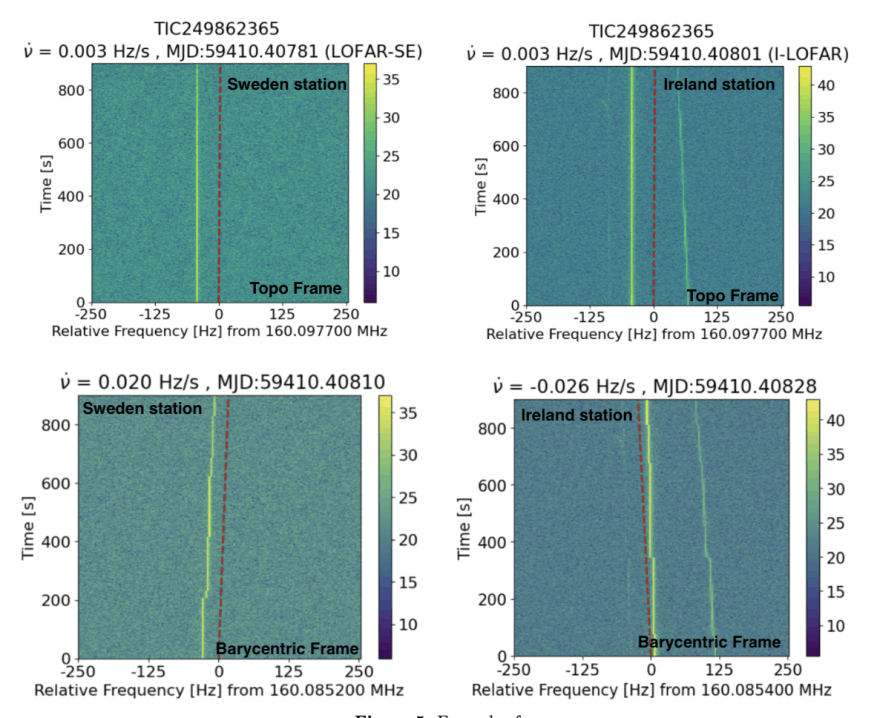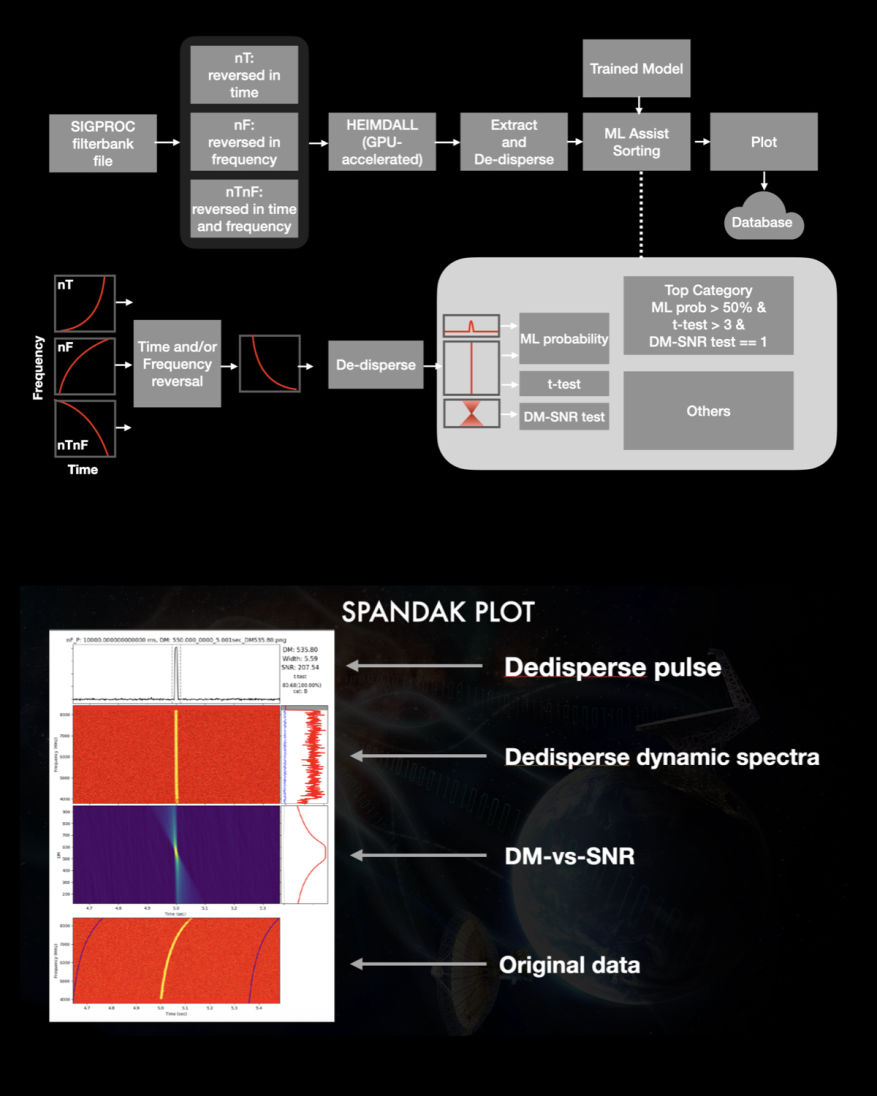
SPANDAK
SPANDAK (in Hindi: pulsating objects) is a python wrapper built around a GPU-accelerated tool — named HEIMDALL (Barsdell et al. 2012) — as the main kernel to search for dispersed signals of natural and artificial origin. It uses a SIGPROC-based filterbank file to search for dispersed pulses from a user-supplied range of DMs and pulse widths. The pipeline accumulates all transient candidates reported with HEIMDALL and cross-references various candidate parameters (proximity of arrival times, DMs, S/Ns, widths, etc.). It removed candidates that appear across a large range of DMs within a short interval, allowing us to remove a significant number of false positives due to RFI. A short list of selected candidates gets extracted from each corresponding filterbank file for further validation. SPADNAK time-scrunches the extracted data such that the detected pulse would fit within two to four-time bins and frequency scrunched 16-512 frequency bins. For candidate validation, the pipeline produces dedispersed dynamic spectra, where an ideal broadband transient pulse should show up across all observed frequencies. The pipeline then selects an on-pulse window based on the width and arrival time reported from HEIMDALL and extracts on-pulse and off-pulse spectra. Pipeline compares the on-pulse and off-pulse spectral energy distribution using a t-test. For a true broadband pulse, the t-test shows a significant difference between these spectra. Moreover, a true broadband dispersed signal shows both a peak at the correct DM and a gradual decline in the S/N around nearby DMs. SPANDAK then produces plots for each of the candidates for visual inspection by the user.